How to find probability in Excel
You can watch a video tutorial here.
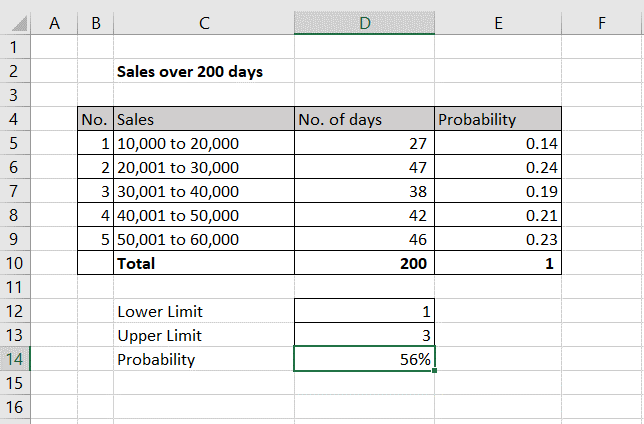
Probability is defined as the likelihood that an event is going to happen. It is the ratio of favorable outcomes of the event to the total number of outcomes of the event. You may want to determine the probability of a particular value of Sales based on historical data. For this, you will need a table with the sales value and the number of instances or the number of days on which the value was reached.
Step 1 – Compute the probability for the first value
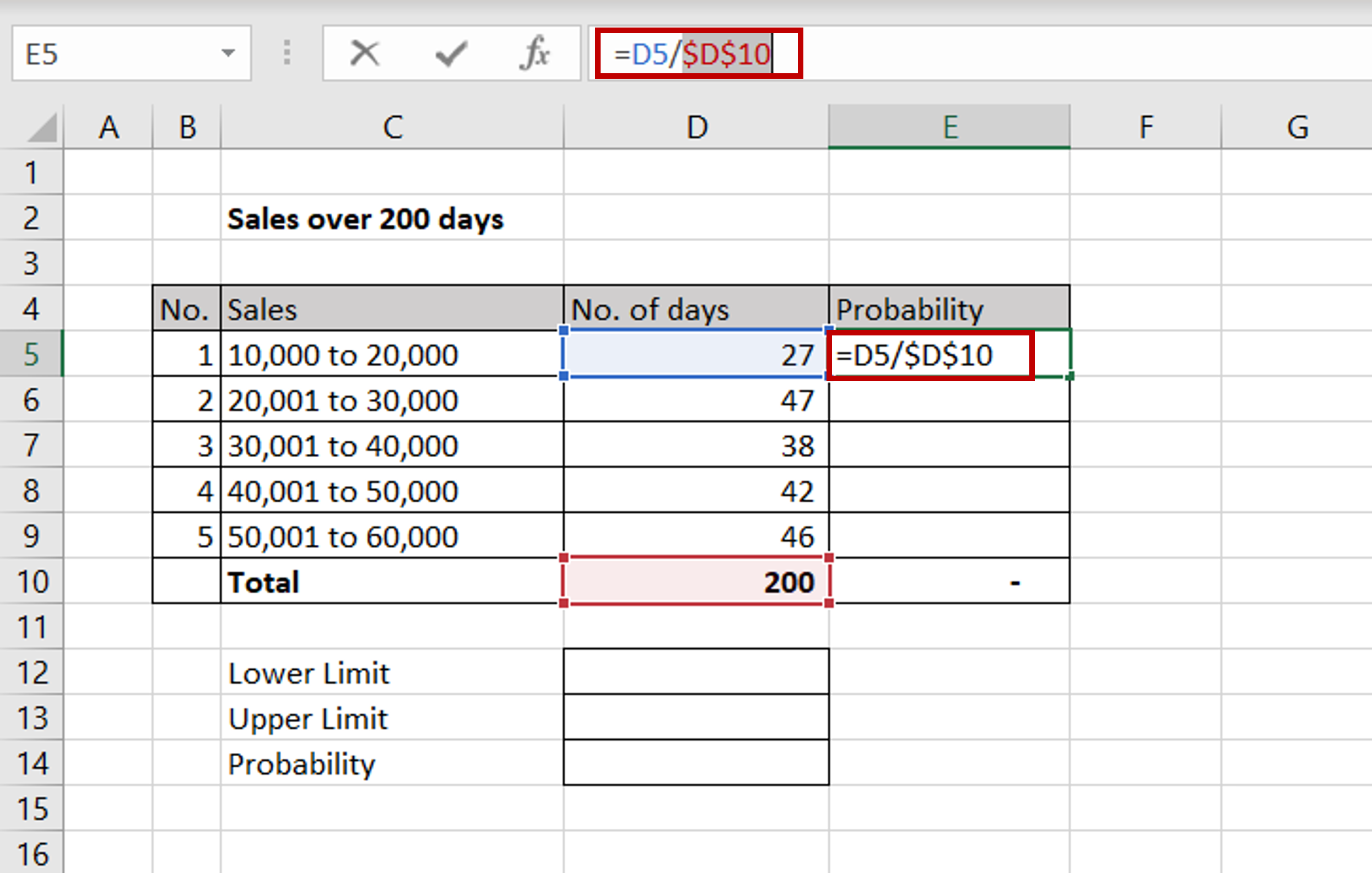
– In the first cell of the ‘Probability’ column, enter the formula:
=<cell reference of the ‘No. of days’ column> / <cell reference of the total ‘No. of days’ column>
Note: This is the formula for probability for a particular event i.e. Number of favorable outcomes/Total number of outcomes
– Make the cell reference for the total ‘No. of days’ constant by selecting the reference and pressing F4 or by typing dollar signs ($) in front of the column and row names
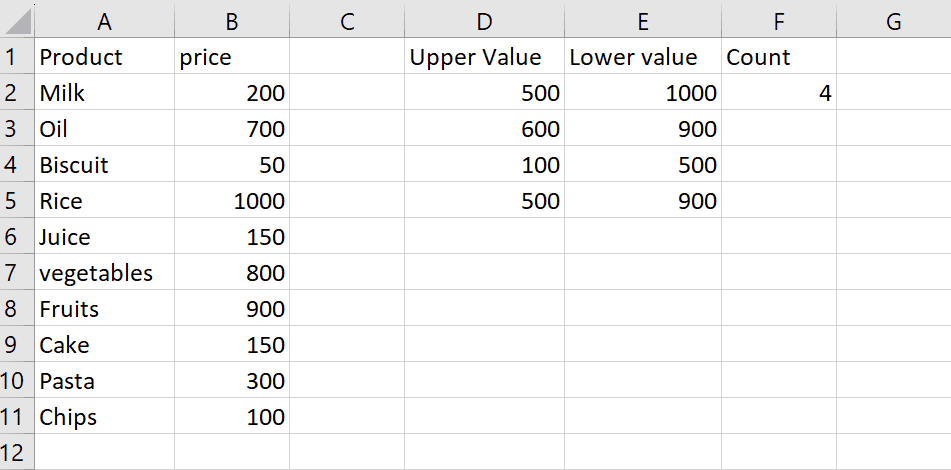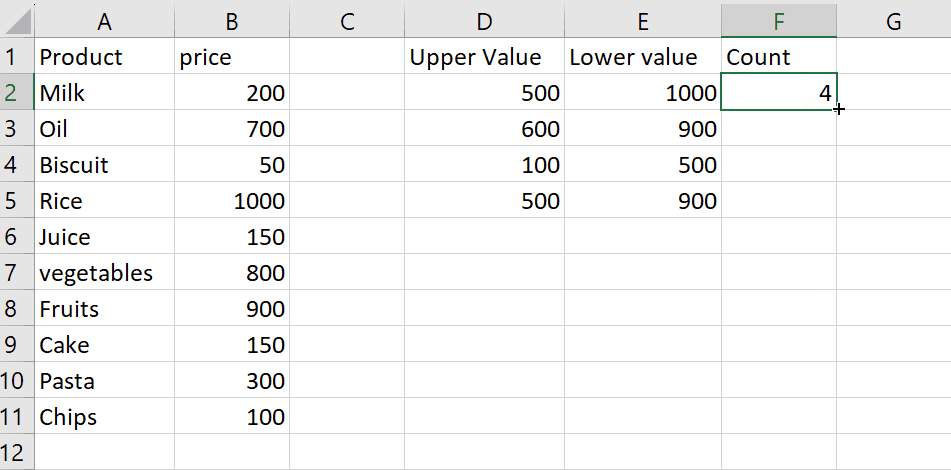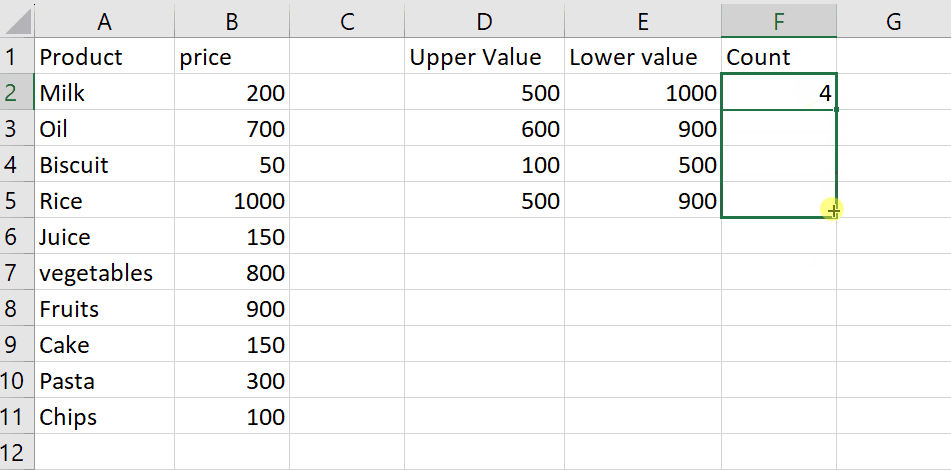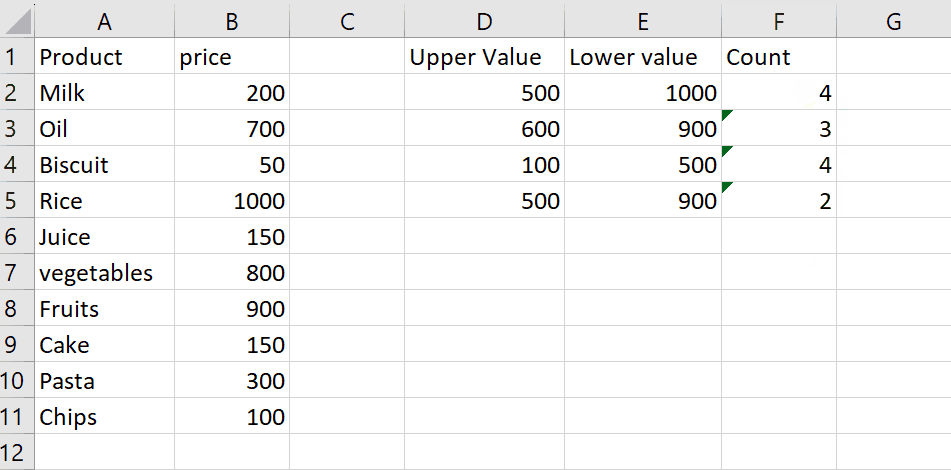
Step 2 – Copy the formula
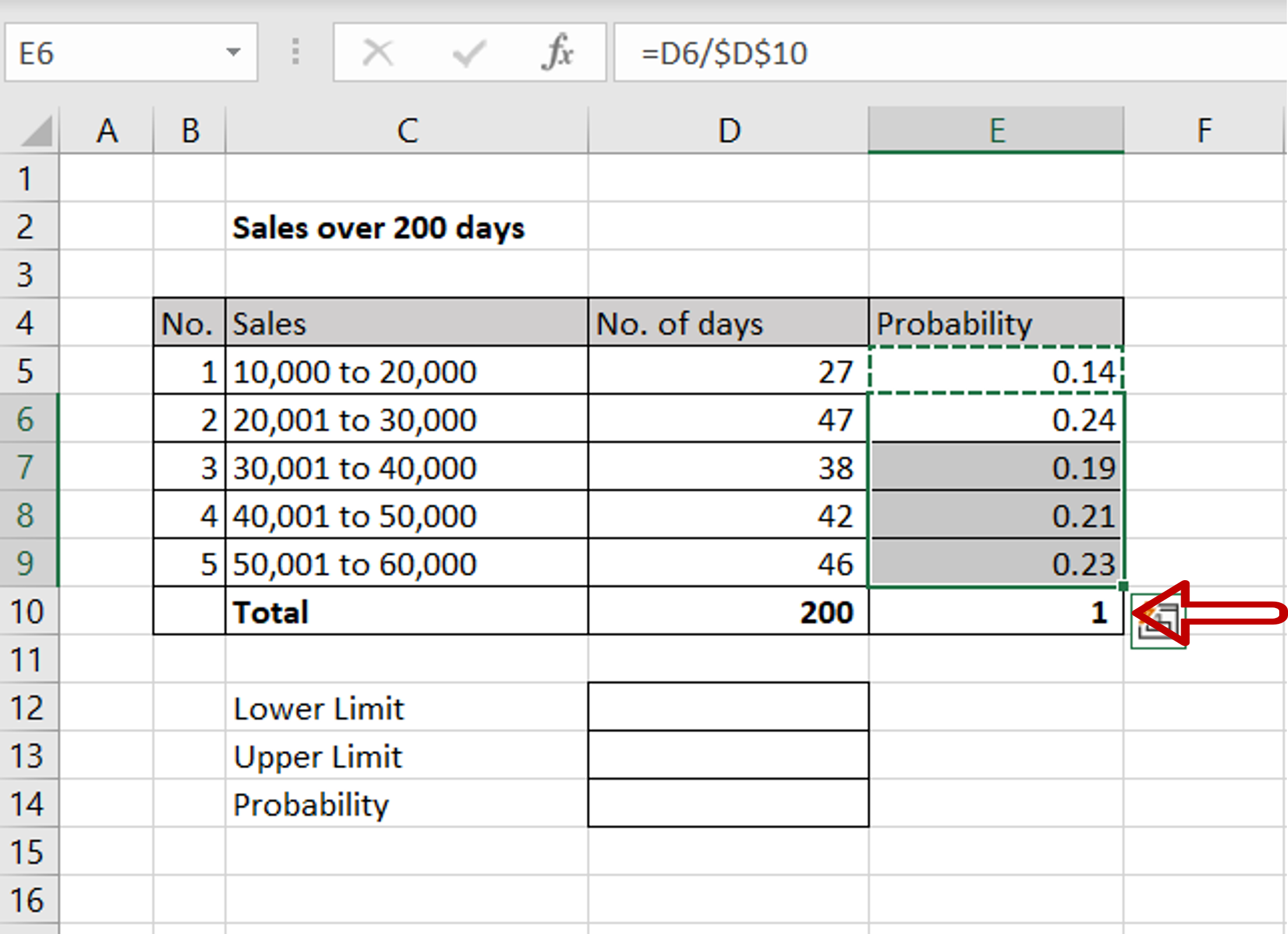
– Using the fill handle from the first cell, drag the formula to the remaining cells
OR
a) Select the cell with the formula and press Ctrl+C or choose Copy from the context menu (right-click)
b) Select the rest of the cells in the column and press Ctrl+V or choose Paste from the context menu (right-click)
– The sum of the ‘Probability’ column must always be 1
Step 3 – Use the PROB() function
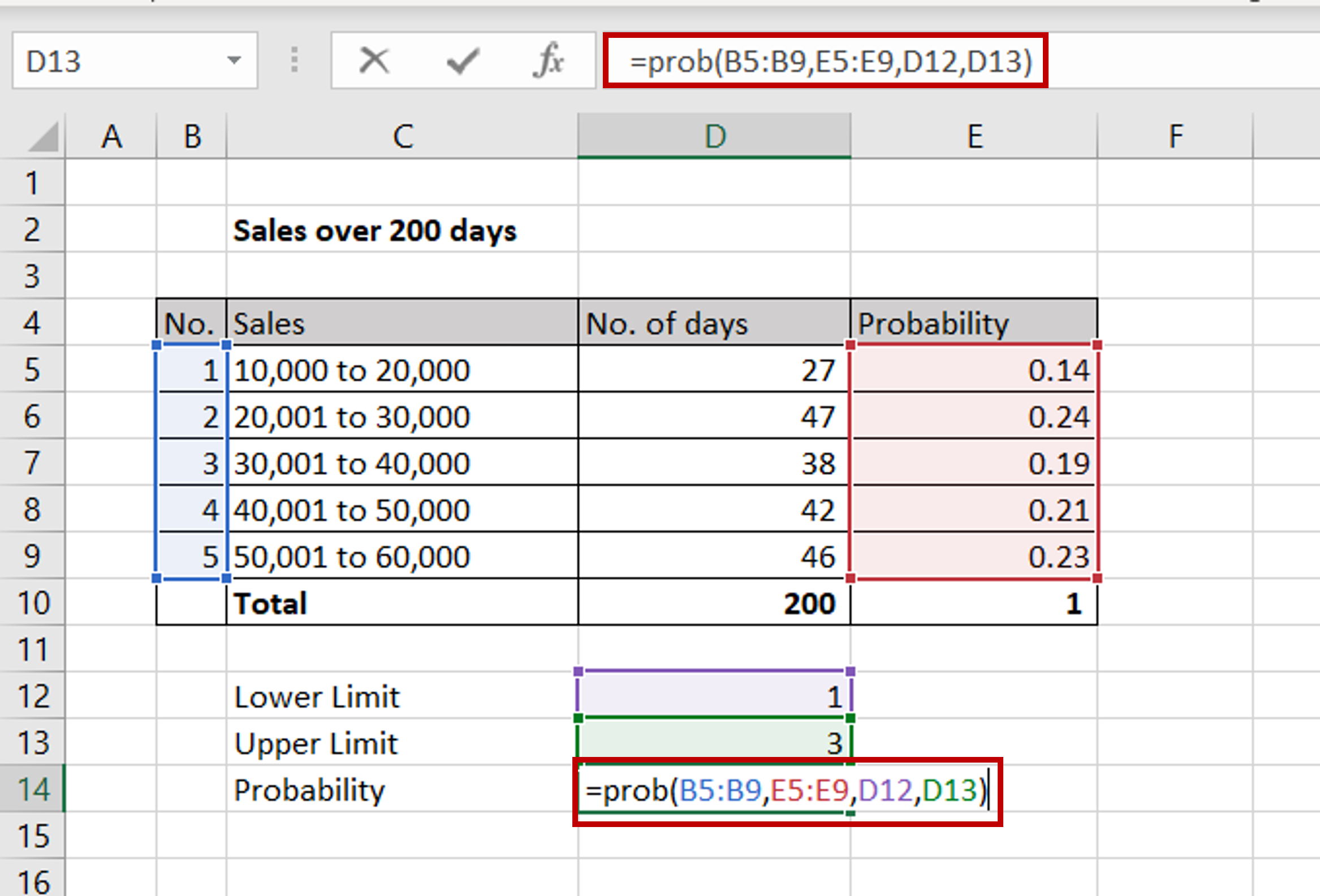
– Define a Lower Limit and an Upper limit using the numbers from the ‘No.’ column
– 1 refers to 10,000 to 20,000 and 3 refers to 30,001 to 40,000
– Enter the formula:
=prob(<range of the ‘No.’ column,
range of the ‘Probability’ column,
cell reference of the Lower Limit,
cell reference of the Upper Limit)
Step 4 – Check the probability of sales value between 10,000 and 40,000
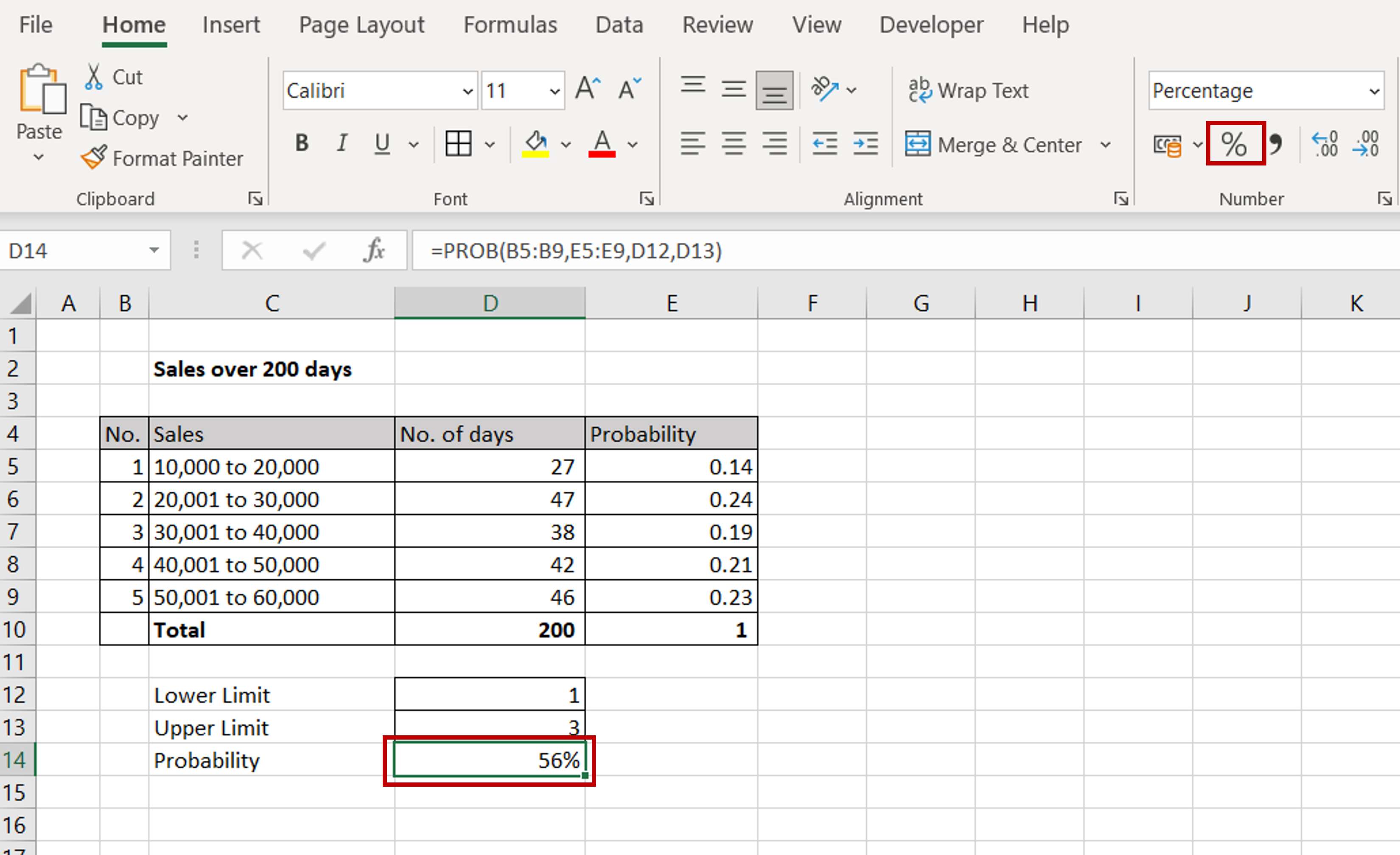
– Format the probability for percentage by using the button on the Home > Number ribbon
– The probability of sales value being between 10,000 and 40,000 is .56 or 56%
– Change the Lower Limit and/or Upper Limit to check the other probabilities
Note: If the Upper Limit is not mentioned, the maximum value in the range is used